| Author |
Message |
    
Socoken
| | Posted on Thursday, August 12, 2004 - 05:54 pm: | 




|
hey, i just noticed that white block in the bottom one!!! how the heck does that work???? its crazy, two triangles, with the same length and height, comprised of the same 4 smaller shapes, and you move them around and BAM! extra space!! thats crazy, must be some sort of trick. |
    
M1combat
| | Posted on Thursday, August 12, 2004 - 05:55 pm: | 




|
Close only counts in horse shoes, hand grenades and nukes. |
    
Newblaster
| | Posted on Thursday, August 12, 2004 - 06:03 pm: | 




|
Socoken--You can read the middle paragraphs of my post to explain the hole. Nevermind the first and last, since they're about triangles, and this isn't one.
M1--That's true. I consider myself herring-slapped.

(Message edited by newblaster on August 12, 2004) |
    
M2me
| | Posted on Thursday, August 12, 2004 - 06:03 pm: | 




|
Ok, I get it now.  |
    
Tucsonxb9s
| | Posted on Thursday, August 12, 2004 - 06:40 pm: | 




|
I still think you guys are over thinking it. Get a piece of paper...make your own dang triangles and polygons....arrange...and re-arrange. I will not be surprised if you get the same result. Theory and conjecture will get you nowhere! Experiment my young Einsteins and see what happens! |
    
M1combat
| | Posted on Thursday, August 12, 2004 - 06:48 pm: | 




|
I would, but if I do indeed get a straight line I will already know that it's because I cut the green and red triangle wrong  . Try cutting each piece out of graph paper to match the dimensions (or number of squares) of each piece. Then, take the green triangle and place it over the left point of the red one and you will see that they are different angles. If you do that though, keep in mind that you will need to have less than a 1.125 degree margin of error on either of the hypotenuse cuts. I recommend making those cuts with a paper cutter. . Try cutting each piece out of graph paper to match the dimensions (or number of squares) of each piece. Then, take the green triangle and place it over the left point of the red one and you will see that they are different angles. If you do that though, keep in mind that you will need to have less than a 1.125 degree margin of error on either of the hypotenuse cuts. I recommend making those cuts with a paper cutter.
Wait... Maybe I can get Z-Modeler to show it... I'll see about that when I get home  . I'm sure Autocad would. . I'm sure Autocad would. |
    
Tucsonxb9s
| | Posted on Thursday, August 12, 2004 - 07:01 pm: | 




|
Good grief! |
    
Crusty
| | Posted on Thursday, August 12, 2004 - 07:09 pm: | 




|
Some people could complicate a Peanut Butter sandwich. |
    
M2me
| | Posted on Thursday, August 12, 2004 - 07:50 pm: | 




|
This isn't as complicated as a peanut butter sandwich but it is plain to see. I cut out the red and green triangles and superimposed them. As you can see they don't line up!
 |
    
Newblaster
| | Posted on Thursday, August 12, 2004 - 07:59 pm: | 




|
A peanut butter sandwich IS complicated... You have to have bread sliced just the right thickness, and then there's the proper ratio of peanut butter to bread, not to mention the kind of thinking you need if you add jelly to the mix... It's really a huge undertaking, nothing to be spoken of lightly.
 |
    
Charlieboy6649
| | Posted on Thursday, August 12, 2004 - 08:58 pm: | 




|
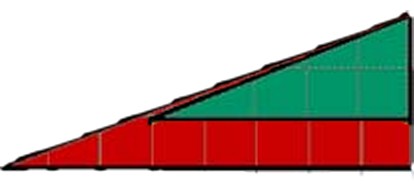
The width of the green triangle 5 squares + the width of the red triangle 8 squares = 13
The two "L" shapes are the same length as the Green triangle... 5
When you switch the red triangle in place of the green 5 + 8 still = 13, but the difference between the red triangle and the "L" shapes, 3, accounts for the gap.
The polygons were initially on top of one another, now they are offset by exactly......3
TaDa!
Time for beer...
(Message edited by charlieboy6649 on August 12, 2004) |
    
Evaddave
| | Posted on Thursday, August 12, 2004 - 11:31 pm: | 




|
Let's look at this from a different perspective. What would it take to make the big triangle truly a triangle? Both of the angles on the left of the smaller triangles would have to be the same, that way the two hypotenuses would make one long, unbroken hypotenuse. Since the left angles are the same, and the right angles are the same, then the top angles also have to be the same, making the red and green triangles congruent.
With congruent triangles, you can find the length of one side on one triangle by comparing the ratio of the sides on the congruent triangle. Let's keep the length and height of the green triangle at 5 and 2, and let's keep the height of the red triangle at 3. The formula would be 5/2 = L/3, and doing some basic algebra, L = 3 * 5/2 = 7.5.
In order for the big figure to be a triangle, the length of the red triangle would be 7.5 blocks, not 8. In the top figure, the left tip of the triangle would be 1/2 block to the right. No big deal. But in the bottom figure, connect the left point of the red triangle to the top point of the green triangle. The shape below the red triangle now sticks out by 1/2 block. Chop off the two half-blocks that are sticking out, and you'll have enough to fill the hole. |
    
M1combat
| | Posted on Thursday, August 12, 2004 - 11:41 pm: | 




|
Yeah... What he said  . . |
    
M1combat
| | Posted on Thursday, August 12, 2004 - 11:43 pm: | 




|
I was making a peanut butter sandwich a while ago and couldn't help myself... I cut it it two congruent triangles... I stuck them to my monitor and neither of them matched the polygon we have above... I think I'll get pizza next time. |
    
Hootowl
| | Posted on Friday, August 13, 2004 - 01:46 am: | 




|
I have found that if you eat the triangles with a glass of milk, the peanut butter doesn't stick so much. |
    
Paulinoz
| | Posted on Friday, August 13, 2004 - 01:48 am: | 




|
Area of Green = 2 x 5/2 = 5 units
Area of Red = 3 x 8/2 = 12 units
Area of Lt green l shape = 8 units
Area of buff l shape =7 units
Total of area 5 + 12 + 8 + 7 = 32 units
That is top triangle = 32 units
Bottom Triangle is 32 + 1 (extra )= 33 units
Area of A large triangle
5 units x 13 units devided by 2 = 32.5 units
ie: what you think are two triangles of the same size in fact are two 4 sided shapes 1 being 1 unit large than the other. |
    
Buellfool
| | Posted on Friday, August 13, 2004 - 01:55 am: | 




|
Hootowl is correct. |
    
Uwgriz
| | Posted on Friday, August 13, 2004 - 11:10 am: | 




|
I'm not usre I follow what Charlieboy6649 is trying to explain. |
    
Tucsonxb9s
| | Posted on Friday, August 13, 2004 - 03:15 pm: | 




|
I still don't get it. I don't think the shapes are four sided, curved, or the angles are different. I think I done and I'm going to have lunch....no peanut butter sandwich either! |
    
Newblaster
| | Posted on Friday, August 13, 2004 - 03:23 pm: | 




|
You know, I did try to make a peanut butter sandwich last night, but the top slice of the bread was a little bit concave on the top. I ended up getting peanut butter everywhere, and now my helmet smells funny. |
    
Uwgriz
| | Posted on Friday, August 13, 2004 - 04:07 pm: | 




|
Tucsonxb9s - the angles are different. It's not a matter of perception. It's geometry. The tangent of the lower left angle in the green triangle is equal to 2/5. Taking the inverse tangent of that yields 21.80°. The tangent of the lower left angle of the red triangle is 3/8. Taking the inverse tangent of that yields 20.56°. The difference is 1.24°, which is small enough that your eye may not pick it up if only casually looking at it. The gridlines get you focused on counting squares and that's how the illusion works. If the bottom side of the red triangle was 7.5 units long or the right side was 3.2 units long or the bottom side of the green triangle was 5-1/3 units long or the right side was 1.875 units long, the angles would be the same and the illusion would not work. Go back to my first posted explanation. It's not a coincedence that the top arrangement has an area of 32, the bottom has an area of 33 and the area of a true triangle of the same base and height dimensions is exactly in the middle at 32.5.
If you still don't believe me, hold a piece of paper perfectly in line with the hypotenuse of the green triangle in M2me's picture above. If you do this you will see that the paper intersects the bottom 1/2 unit to the right of the tip of the red triangle. |
|